You can calculate the position of one of the major planets to within an accuracy of one arc minute on the sky using an ordinary scientific calculator in about 20 minutes.
You will need the current 'osculating elements' for the elliptical orbit of the planet and for the Earth. Osculating elements allow for the effects of the mutual interactions of the planets for a given date, and positions calculated from a given set of elements will be less accurate further from that date. The advantage is in conceptual simplicity - you are using a simple 2- body model of an orbit, with the Sun at one focus.
I shall calculate the position of Mars as an example, and the positions will be within a few arc minutes of the correct positions for about a year either side of the date of the elements used.
You might want to find a position 'by hand' once, so as to
understand the calculation method and get a feel for the size of
the numbers involved. After that, it is fairly easy to write a
simple program for a programmable calculator, or devise a
spreadsheet. A very simple QBASIC program is given
below.
The image of an elliptical orbit moving under Kepler's laws seems so simple that we forget how confused and difficult the development of this idea was. To mention just one detail - in the period after Kepler and before Newton, there was no good theory of atmospheric refraction, so that reported positions of the planets had systematic errors which depended on the angle above the horizon at which the observations were made. Observations would not fit ellipses in a consistent way, and Kepler, Horrocks and Streete (to name a few) struggled with 'anomalies' in the sense of Kuhn [Kuhn 1962].
The positions of objects in the sky as viewed from Earth are referred to a coordinate system whose alignment is changing with time in a complex way. A few of the important motions and effects are summarised below;
The 'fixed' stars provide a reference system which allows us to account for the daily rotation of the Earth on its axis. We use the Equatorial coordinate system to refer positions to a frame in which the stars appear still, and the right ascension (RA) and declination (DEC) are used to give the coordinates of the planet with respect to the fixed stars. The 'zero' of RA is refered to the 'vernal equinox', in the same way that the 'zero' of longitude is taken as the Greenwich Meridian.
The presession of the equinoxes means that the 'zero' of RA is changing slowly with time, which means that star coordinates must always be referred to an epoch, or date. By using orbital elements referred to the fundamental epoch J2000, the orbits of the planets are described in a coordinate system which is based on the position the vernal equinox will have at J2000. A further advantage of this dodge is that our positions for the planets will correspond exactly to the positions found in most recent star charts. You should be able to plot the path of Mars directly onto a star chart such as The Cambridge Star Atlas.
Nutation (which is a small effect anyway) can also be spirited away by referring our positions to the 'mean ecliptic of J2000'. The word 'mean' indicates that no allowance for nutation has been made. Our observation platform (the Earth) is nodding, so the stars and planets will appear to nod together. Our J2000 elements will give is positions which match the co-ordinates of the stars found in star maps.
There is a problem with this use of J2000 equinox and mean ecliptic. If I just dial the values for RA and DEC into a computerised telescope, then the planet will not appear in the centre of the field of view - as the RA and DEC will not be referred to the 'equinox and true ecliptic of date'. The effect will be very small for 10 years either side of J2000.
A larger effect with the outlying planets will be caused by the finite speed of light. Indeed, one of the first estimates of the speed of light was obtained by careful timings of the eclipses of the Galilean moons of Jupiter. Light takes about 50 minutes to reach us from Jupiter, and so we see Jupiter in a position it was about 50 minutes before we looked! The problem is that we don't know how far Jupiter is until we calculate the planet's position, but we can't calculate the position accurately until we allow for the light travel time.... A series of approximations is needed. A position which has been corrected for the light travel time and which is referred to equinox and mean ecliptic of J2000 is called 'astrometric'. I shall be adding corrections for this later.
There are approximate and accurate formulas for converting positions at one time to positions at another [Duffett-Smith section 34, 35] [Meeus, Chapter 20, 21].
For more information on frames and rectangular coordinates, including some rather nice diagrams, see;
http://ph1.rmc.ca/~deboer/om/frame/frame.html
An elliptical orbit can be specified by the values of various numbers. The plane of the orbit must be specified, as must the size and the eccentricity, and the position of the perihelion, and the position of the planet at the date of the elements. There are a number of different sets of numbers which can be used, and one set can be converted into another set. The Astronomical Almanac provides 7 numbers to specify an orbit;
I use the osculating elements taken from page E3 of the Astronomical Almanac for 1997. As explained in the previous section, these elements are referred to the 'mean ecliptic and equinox' of J2000.0, so that positions calculated from these elements will show the correct relationship with the stars when plotted on a J2000 star chart, apart from the effect of light travel time. The osculating elements include the effects of the other planets (perturbations) at the date 8th August 1997, and will give less accurate positions the further we go from that date. This has nothing to do with the coordinate system we happen to want to use, the J2000 mean ecliptic and equinox.
JD = 2450680.5
Equinox and mean ecliptic of J2000.0
Earth Mars
i 0.00041 1.84992
o 349.2 49.5664
p 102.8517 336.0882
a 1.0000200 1.5236365
n 0.9855796 0.5240613
e 0.0166967 0.0934231
L 328.40353 262.42784
The values for the other planets can be found in
the QBASIC program below
The sections below deal with calculating the RA and DEC of a planet from the osculating elements. As an example, I shall find the position of Mars at 0h UT on the 21st of June 1997. The main steps in the calculation are;
I have used rectangular coordinates throughout, as most people with a science and engineering background will be more familiar with the ideas of coordinate transformations acting on Cartesian coordinates than with spherical trigonometry. Those who know matrix algebra might feel happier recasting the calculations below in matrix form [Duffett-Smith, section 31]. The method shown here is not that used by Thomas Streete or Edmond Halley!
The method used here was adapted from Paul Schlyter's page 'How to compute planetary positions' at
http://hotel04.ausys.se/pausch/comp/ppcomp.html
Elements i - inclination o - longitude of ascending node at date of elements p - longitude of perihelion at date of elements a - mean distance (au) n - daily motion e - eccentricity of orbit l - mean longitude at date of elements Calculated quantities M - mean anomaly (degrees) V - True anomaly (degrees) r - radius vector (au) referred to current coordinate origin X - recangular coordinate (au) Y - recangular coordinate (au) Z - recangular coordinate (au) alpha - right ascension (hours or decimal degrees according to context) delta - declination (decimal degrees)
To find the number of days since the date of the osculating elements (d), you can find the 'day number' (dele) of the elements, and then the 'day number' you want the position for (dpos). Then you just subtract,
d = dpos - dele
The 'day number' can be the Julian day, or the number of days since the fundamental epoch J2000. I use the second alternative as less precision is needed for the numbers!
The following tables show the days from the beginning of the year to the beginning of each month, and the days from J2000 to the beginning of each year.
Days to beginning of month
Month Normal year Leap year
Jan 0 0
Feb 31 31
Mar 59 60
Apr 90 91
May 120 121
Jun 151 152
Jul 181 182
Aug 212 213
Sep 243 244
Oct 273 274
Nov 304 305
Dec 334 335
Days since J2000 to beginning of each year
Days
1995 -1827.5
1996 -1462.5
1997 -1096.5
1998 -731.5
1999 -366.5
2000 -1.5
2001 364.5
2002 729.5
2003 1094.5
2004 1459.5
2005 1825.5
we can find the day number corresponding to the date of the elements (0h 20th August 1997) as follows;
dele = 212 + 20 - 1096.5 = -864.5
and the day number of the date we want the position for (0h 21st June 1997) is;
dpos = 151 + 21 - 1096.5 = -924.5
so the number of days after the date of the elements is
dpos - dele = d
-924.5 - -864.5 = -60 days
i.e. 60 days before the elements. You must take dates
before an epoch as negative in the calculations below.
For fast moving planets such as Mercury and Mars, you need to include the time of day which you want the position for. Just add the Universal Time in decimal hours divided by 24 to the day number of your position (dele above);
day fraction = (H + M/60)/24
H is hours UT
M is minutes UT
The Mean Anomaly of the planet is given by the very simple formula;
M = n * d + L - p
n is daily motion
d is the number of days since the date of the elements
L is the mean longitude
p is the longitude of perihelion
M should be in range 0 to 360 degrees, add or subtract
multiples of 360 to bring M into this range.
For our case of Mars and -60 days since the date of the elements;
n = 0.5240613
d = -60
L = 262.42784
p = 336.0882
M = 0.5240613 * -60 + 262.42784 - 336.0882
= -105.104038 + 360
= 254.895962
Kepler's second law states that the radius vector of the planet sweeps out equal areas in equal times. This means that the planet must speed up and slow down in its orbit. The mean anomaly tells us where the planet would be given mean motion in a circular orbit of radius equal to the semimajor axis. We want the true angle from the perihelion - known as the true anomaly.
For this 'manual' calculation, I shall use an approximation to the true anomaly known as the Equation of Centre. This approximation takes the form of a power series in the eccentricity and the sine of the mean anomaly. The Astronomical Almanac (page E4) quotes the series as far as the third power of the eccentricity. In our notation;
v = M + 180/pi * [ (2 * e - e^3/4) * sin(M)
+ 5/4 * e^2 * sin(2*M)
+ 13/12 * e^3 * sin(3*M) ]
v is true anomaly
M is mean anomaly
e is eccentricity
pi is 3.14159...
e^3 means the third power of e. Note how the third
power is involved the first term as well as the last.
For our Mars position, we have
M = 254.895962 degrees
e = 0.0934231
v = 254.895962 + 57.29577951 * [ -0.180195 + 0.005489 +
0.0006212 ]
= 254.895962 - 9.974293328
= 244.921657 degrees
As you can see, the correction is large for Mars, nearly 10
degrees. I usually do a rough check on the size of this
correction - find a rough value for 2 * e * sin(M)
then multiply by 60.
For more information about the true anomaly, see my page at;
http://www.geocities.com/CapeCanaveral/Lab/4749/kepler.html
The distance from the planet to the focus of the ellipse is given by a simple formula based on the geometry of the ellipse;
r = a * (1 - e^2) / [1 + e * cos(v)]
a is the semi-major axis
e is the eccentricity
v is the true anomaly
the radius vector r will be in the same units as a
a.u. in this case.
In our Mars calculation we have;
a = 1.5236365
e = 0.0934231
v = 244.921657
r = 1.5236365 * (1 - 0.0934231^2) / [ 1 + 0.0934231 * cos
(244.921657) ]
= 1.57261067
Having found the true anomaly and the radius vector of the planet, we can go on to find the position of the planet with respect to the plane of the ecliptic. The formulas below are a combination of 'resolving' to find components and rotations around various axes to transform the coordinates to the Ecliptic frame. We might expect the formulas to involve the inclination of the planet's orbit (i), and various angles within the plane of the orbit, as well as the longitude of the ascending node (o).
X = r * [cos(o) * cos(v + p - o) - sin(o) * sin(v + p - o) *
cos(i)]
Y = r * [sin(o) * cos(v + p - o) + cos(o) * sin(v + p - o) *
cos(i)]
Z = r * [sin(v + p - o) * sin(i)]
r is radius vector
v is true anomaly
o is longitude of ascending node
p is longitude of perihelion
i is inclination of plane of orbit
the quantity v + o - p is the angle of the planet measured
in the plane of the orbit from the ascending node
In the case of Mars we have;
r = 1.57261067
v = 244.921657
o = 49.5664
p = 336.0882
i = 1.84992
v + p - o = 531.443457 - 360 = 171.443457
and I get the following rectangular coordinates;
X = 1.57261067 * [ -0.64134752 - 0.11319000 ] = -1.18659376
Y = 1.57261067 * [ -0.75268604 + 0.09644689 ] = -1.03200869
Z = 1.57261067 * [ 0.00480302 ] = 0.00755328
as a check, SQRT(X^2 + Y^2 + Z^2) should be same as r
I get a difference in the 7th decimal place due to
rounding.
We must find the true anomaly and radius vector of the Earth using the same method as for the planet. The calculations are shown in a more compact form - see if you can follow the logic.
M = 0.9855796 * -60 + 328.40353 - 102.8517
= 166.417054 degrees
V = 166.417054 + 57.29577951 * [ 0.00784226 - 0.00015852 +
0.00000328 ]
= 166.417054 + 0.440433803
= 166.8574877
(note how small the difference between M and v is
compared
to the difference for Mars)
r = 1.0000200 * (1 - 0.0166967^2) / [1 + 0.0166967 *
cos(166.8574877)]
= 1.01626505 a.u.
To find the heliocentric coordinates for Earth, we can make some simplifications to the formulas as the inclination of the Earth's orbit is very small. We have;
Xe = r * cos(v + p) Ye = r * sin(v + p) Ze = 0 r is radius vector of Earth v is true anomaly for Earth p is longitude of perihelion for Earth
For the problem in hand we have;
r = 1.01626505 a.u. v = 166.8574877 degs p = 102.8517 degs Xe = 1.01626505 * -0.0050756103 = -0.00515816 Ye = 1.01626505 * -0.999987119 = -1.01625196 Ze = 0
Changing the origin of the coordinate system from the Sun to the Earth is very easy, we just subtract the Earth's coordinates from those of the planet;
X' = X - Xe Y' = Y - Ye Z' = Z - Ze
We then have the geocentric ecliptic coordinates of the planet. For the case of Mars we have,
X' = -1.18659376 - -0.00515816 = -1.18143560 Y' = -1.03200869 - -1.01625196 = -0.01575673 Z' = 0.00755328 - 0 = 0.00755328
To change the coordinate system from geocentric ecliptic to geocentric equatorial is just a matter of a rotation around the X axis by an angle equal to the 'obliquity of the Ecliptic. The X axis points towards the 'First point of Aries', which is the direction in space associated with the equinox. As we are using elements referred to the equinox of J2000.0, we use the obliquity for that epoch, which is 23.439292 degrees. the formulas are given below;
Xq = X'
Yq = Y' * cos(ec) - Z' * sin(ec)
Zq = Y' * sin(ec) + Z' * cos(ec)
Xq are the equatorial coordinates
X' are the geocentric ecliptic coordinates
ec is the obliquity of the ecliptic
For Mars, we have
Xq = -1.18143560
Yq = -0.01746127
Zq = +0.00066224
rectangular coordinates are not much use with star charts, so we calculate the familiar right ascension and declination using the formulas;
alpha = arctan(Yq/Xq)
If Xq is negative then add 180 degrees to alpha
If Xq is positive and Yq is negative then add 360 degrees to
alpha
alpha is usually expressed in hours, so divide by 15
delta = arctan( Zq / SQRT(Xq^2 + Yq^2))
distance = SQRT( Xq^2 + Yq^2 + Zq^2)
In the case of Mars on the 21st June 1997 we have
alpha = arctan(-0.01746127/-1.18143560)
= 0.84675309 + 180 = 180.84675309 /15
= 12.05645 hrs
delta = arctan(+0.00066224/ 1.39609497)
= 0.02718 degs
distance = SQRT( -1.18143560^2 + -0.01746127^2 +
+0.00066224^2)
= 1.18156481 a.u.
These positions compare well with those from the
QBASIC program, which uses an iterative routine to
find the true anomaly. Differences in the heliocentric
coordinates of Mars are in the fourth decimal place. Differences
in the RA are five arc minutes and about 20 arc seconds
in
declination.
The very simple QBASIC program below will prompt
you
for the Year, Month, Day and Hour and Minute (UT) for which you
want the position, and a number representing the planet you wish
to calculate the position for. The program will then print
I have used the DEF FN statements to define
functions. By
doing this the code will compile using the FirstBas shareware
compiler available from PowerBasic.
'*********************************************************
' This program will calculate the positions of the
' major planets using the current 'osculating elements'
' from the Astronomical Almanac.
'
' A simple elliptical orbit
' is assumed for both the planet and the Earth - no
' corrections are made from within the program as the
' osculating elements will already take account of
' perturbations.
'
' The method used here is based on finding the rectangular
' coordinates of the planet and of the Earth, and then
applying
' successive coordinate transformations to find the
rectangular
' gocentric equatorial coordinates of the planet.
'
' QBASIC program by Keith Burnett (kburnett@geocity.com)
'
'
' Work in double precision and define some constants
'
DEFDBL A-Z
pr$ = "\ \#####.##"
pr2$ = "\ \###.######"
pi = 4 * ATN(1)
tpi = 2 * pi
twopi = tpi
degs = 180 / pi
rads = pi / 180
'
' list of elements el()
' List of the osculating elements of the 9 major
' planets in the format used in the Astronomical
' Ephemeris. Item el(64) in list is the Julian date
' of the elements. Item el(65) is the epoch of the
' mean ecliptic and equinox the elements are referred to.
'
' If you want positions referred to
' the mean equator and equinox of the date of the
' osculating elements, then use the elements listed
' on pages E4 and E5 of the AA. If you want the positions
' referred to the mean equator and equinox of J2000
' then use the elements found on page E3 of the AA.
'
'
DIM el(9 * 7 + 2)
' below are the osculating elements for JD = 2450680.5
' referred to mean ecliptic and equinox of J2000
'Mercury
el(1) = 7.00507# * rads
el(2) = 48.3339# * rads
el(3) = 77.45399999999999# * rads
el(4) = .3870978#
el(5) = 4.092353# * rads
el(6) = .2056324#
el(7) = 314.42369# * rads
'Venus
el(8) = 3.39472# * rads
el(9) = 76.6889# * rads
el(10) = 131.761# * rads
el(11) = .7233238#
el(12) = 1.602158# * rads
el(13) = .0067933#
el(14) = 236.94045# * rads
'Earth
el(15) = .00041# * rads
el(16) = 349.2# * rads
el(17) = 102.8517# * rads
el(18) = 1.00002#
el(19) = .9855796# * rads
el(20) = .0166967#
el(21) = 328.40353# * rads
'Mars
el(22) = 1.84992# * rads
el(23) = 49.5664# * rads
el(24) = 336.0882# * rads
el(25) = 1.5236365#
el(26) = .5240613# * rads
el(27) = .0934231#
el(28) = 262.42784# * rads
'Jupiter
el(29) = 1.30463# * rads
el(30) = 100.4713# * rads
el(31) = 15.6978# * rads
el(32) = 5.202597#
el(33) = 8.309618000000001D-02 * rads
el(34) = .0484646#
el(35) = 322.55983# * rads
'Saturn
el(36) = 2.48524# * rads
el(37) = 113.6358# * rads
el(38) = 88.863# * rads
el(39) = 9.571899999999999#
el(40) = .03328656# * rads
el(41) = .0531651#
el(42) = 20.95759# * rads
'Uranus
el(43) = .77343# * rads
el(44) = 74.0954# * rads
el(45) = 175.6807# * rads
el(46) = 19.30181#
el(47) = .01162295# * rads
el(48) = .0428959#
el(49) = 303.18967# * rads
'Neptune
el(50) = 1.7681# * rads
el(51) = 131.7925# * rads
el(52) = 7.206# * rads
el(53) = 30.26664#
el(54) = .005919282# * rads
el(55) = .0102981#
el(56) = 299.8641# * rads
'Pluto
el(57) = 17.12137# * rads
el(58) = 110.3833# * rads
el(59) = 224.8025# * rads
el(60) = 39.5804#
el(61) = .003958072# * rads
el(62) = .2501272#
el(63) = 235.7656# * rads
'Dates
el(64) = 2450680.5# 'date of elements
el(65) = 2451545# 'date of mean ecliptic and equinox of
elements
'
' Get the days to J2000
' h is UT in decimal hours
' FNday only works between 1901 to 2099 - see Meeus chapter 7
'
DEF FNday (y, m, d, h) = 367 * y - 7 * (y + (m + 9) \ 12) \ 4 +
275 * m \ 9 + d - 730531.5 + h / 24
'
' define some arc cos and arc sin functions and a modified
inverse
' tangent function
'
DEF FNacos (x)
s = SQR(1 - x * x)
FNacos = ATN(s / x)
END DEF
DEF FNasin (x)
c = SQR(1 - x * x)
FNasin = ATN(x / c)
END DEF
'
' the atn2 function below returns an angle in the range 0 to
two pi
' depending on the signs of x and y.
'
DEF FNatn2 (y, x)
a = ATN(y / x)
IF x < 0 THEN a = a + pi
IF (y < 0) AND (x > 0) THEN a = a + tpi
FNatn2 = a
END DEF
'
' the function below returns the true integer part,
' even for negative numbers
'
DEF FNipart (x) = SGN(x) * INT(ABS(x))
'
' the function below returns an angle in the range
' 0 to two pi
'
DEF FNrange (x)
b = x / tpi
a = tpi * (b - FNipart(b))
IF a < 0 THEN a = tpi + a
FNrange = a
END DEF
'
DEF FNkep (m, ecc, eps)
'
' returns the true anomaly given
' m - the mean anomaly in radians
' ecc - the eccentricity of the orbit
' eps - the convergence paramter (8 or 9 is usually fine
' 12 or 14 for very accurate work)
'
e = m
delta = .05#
DO WHILE ABS(delta) >= 10 ^ -eps
delta = e - ecc * SIN(e) - m
e = e - delta / (1 - ecc * COS(e))
LOOP
v = 2 * ATN(((1 + ecc) / (1 - ecc)) ^ .5 * TAN(.5 * e))
IF v < 0 THEN v = v + tpi
FNkep = v
END DEF
'
DEF FNdegmin (x)
' cosmetic function returns angular values as a made up
decimal
' number - ddd.mm - the digits after the decimal point are
the
' minutes.
a = FNipart(x)
b = x - a
e = FNipart(60 * b)
' deal with carry on minutes
IF e >= 60 THEN
e = 0
a = a + 1
END IF
FNdegmin = a + e / 100
END DEF
'
CLS
'
' get the date and planet number from the user
'
INPUT " year : ", y
INPUT " month : ", m
INPUT " day : ", day
INPUT " hour UT : ", h
INPUT " minute : ", mins
h = h + mins / 60
INPUT " planet : ", p
d = FNday(y, m, day, h)
PRINT USING pr$; " days : "; d
'
' get the osculating elements from the list
' using letters instead of the array element
' makes the program easier to read.
'
q = 7 * (p - 1)
ip = el(q + 1)
op = el(q + 2)
pp = el(q + 3)
ap = el(q + 4)
np = el(q + 5)
ep = el(q + 6)
lp = el(q + 7)
ie = el(15)
oe = el(16)
pe = el(17)
ae = el(18)
ne = el(19)
ee = el(20)
le = el(21)
eldate = el(64) - 2451545#
'
' now find position of Earth in orbit
'
me = FNrange(ne * (d - eldate) + le - pe)
ve = FNkep(me, ee, 12)
re = ae * (1 - ee * ee) / (1 + ee * COS(ve))
xe = re * COS(ve + pe)
ye = re * SIN(ve + pe)
ze = 0
PRINT
PRINT "heliocentric coordinates of Earth"
PRINT USING pr2$; " X :"; xe
PRINT USING pr2$; " Y :"; ye
PRINT USING pr2$; " Z :"; ze
'
' and position of planet in its orbit
'
mp = FNrange(np * (d - eldate) + lp - pp)
vp = FNkep(mp, ep, 12)
rp = ap * (1 - ep * ep) / (1 + ep * COS(vp))
'
' heliocentric rectangular coordinates of planet
'
xh = rp * (COS(op) * COS(vp + pp - op) - SIN(op) * SIN(vp + pp -
op) * COS(ip))
yh = rp * (SIN(op) * COS(vp + pp - op) + COS(op) * SIN(vp + pp -
op) * COS(ip))
zh = rp * (SIN(vp + pp - op) * SIN(ip))
PRINT
PRINT "heliocentric coordinates of Planet"
PRINT USING pr2$; " X :"; xh
PRINT USING pr2$; " Y :"; yh
PRINT USING pr2$; " Z :"; zh
'
' convert to geocentric rectangular coordinates
'
xg = xh - xe
yg = yh - ye
zg = zh
'
' rotate around x axis from ecliptic to equatorial coords
'
ecl = 23.429292# * rads# 'value for J2000.0 frame
xeq = xg
yeq = yg * COS(ecl) - zg * SIN(ecl)
zeq = yg * SIN(ecl) + zg * COS(ecl)
'
' find the RA and DEC from the rectangular equatorial coords
'
ra = FNatn2(yeq, xeq)
dec = ATN(zeq / SQR(xeq * xeq + yeq * yeq))
rvec = SQR(xeq * xeq + yeq * yeq + zeq * zeq)
PRINT
PRINT "Equatorial coordinates of planet"
PRINT USING pr$; " RA : "; FNdegmin(ra * degs / 15)
PRINT USING pr$; " DEC : "; FNdegmin(dec * degs)
PRINT USING pr2$; "Distance : "; rvec
END
'*********************************************************
Below is a sample of the output of the program - the position of
Mars for 0h UT 21st June 1997.
year : 1997
month : 6
day : 21
hour UT : 0
minute : 0
planet : 4
days : -924.50
heliocentric coordinates of Earth
X : -0.005159
Y : -1.016252
Z : 0.000000
heliocentric coordinates of Planet
X : -1.186699
Y : -1.031907
Z : 0.007558
Equatorial coordinates of planet
RA : 12.03
DEC : 0.02
Distance : 1.181669
The QBASIC program was modified to produce
positions for the major panets over a 20 year period centred on
the date of the osculating elements used. The resulting
positions
were saved to a file and loaded into a spreadsheet long with
values exported from Planeph 2.1, which was set to generate
positions referred to the 'mean ecliptic and equinox of
J2000.0'.
The Error was defined as 'value from osculating elements - value
from Planeph'. Remember that the program uses an accurate
iterative method for finding the true anomalies of both the
planet and Earth.
The results are shown in the table below. I forgot that my
QBASIC program was rounding the RA and DEC figures
to three decimal places, so errors smaller than 2 seconds or
arcseconds could really be anywhere between 0 and 2
seconds/arcseconds!
Errors in RA in seconds of time
+- 1 year +- 3 years +- 10 years
RMS Max RMS Max RMS Max
Mercury 3 8 5 18 17 60
Venus 2 4 8 31 27 135
Mars 2 4 5 15 26 130
Jupiter 1 2 1 4 16 50
Saturn 1 2 3 10 58 180
Uranus 1 2 1 3 8 20
Neptune 1 2 2 4 7 18
Pluto 1 2 2 5 6 13
Errors in DEC in arc-seconds
+- 1 year +- 3 years +- 10 years
RMS Max RMS Max RMS Max
Mercury 15 38 21 70 69 258
Venus 7 15 37 158 98 639
Mars 8 17 24 80 145 832
Jupiter 3 8 4 11 75 265
Saturn 2 3 12 29 194 789
Uranus 2 4 4 15 41 114
Neptune 1 2 3 9 28 80
Pluto 2 4 5 15 33 83
The longer period planets (beyond Jupiter) may show larger errors for other choices of element date - the 20 year time span here is only sampling part of a typical orbit, and Saturn, Uranus and Neptune are strongly perturbed by Jupiter.
With 'peak to mean ratios' like those in the table, you might guess that a time series graph of error against position date would show a complex behaviour, not a simple monotonic rise with time from the date of the elements. Looking at the plots of error against decimal year from the date of the elements does indeed show a complex periodic structure. Below are the plots for Mars.
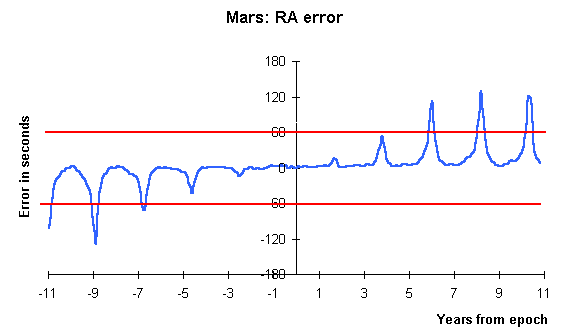
The main features of the RA error time series for Mars are
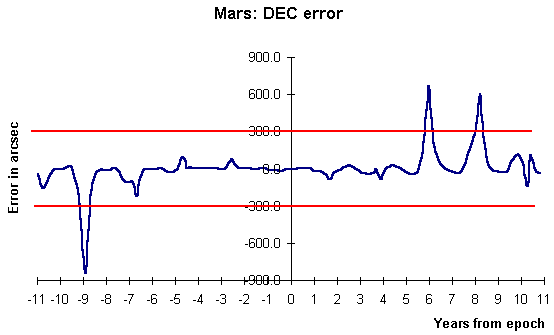
The main features of the DEC error time series for Mars are;
Below is a list of the books which I have used in compiling this page. These books should be found in most University libraries in English speaking countries.
Duffett-Smith, Peter
Practical Astronomy with your calculator
Cambridge University Press
3rd edition 1988
ISBN 0-521-35699-7
Kuhn, Thomas S
The Structure of Scientific Revolutions
2nd Ed, 1972
University of Chicago Press
ISBN 0-226-45804-0
Meeus, Jean
Astronomical Algorithms
Willmann-Bell
1st English edition, 1991
ISBN 0-943396-35-2
[Root]
Last Modified 26th July 1998
Corrected a problem with the equation of centre formula,
pointed out by Donald Thompson.
Keith Burnett