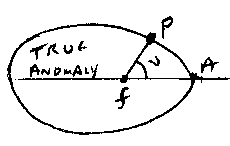
'Since I was aware that there exists an infinite number of points
on the orbit and accordingly an infinite number of distances [from
the Sun] the idea occured to me that the sum of these distances
is contained in the area of the orbit. For I remembered
that in the same manner Archimedes too divided the area of a
circle into an infinite number of triangles'
-Kepler
This page deals with the problem of finding the true anomaly for a planet in an elliptical orbit around the Sun. I describe three methods for finding the true anomaly from the mean anomaly and the eccentricity of the orbit;
If you can stand an error of half a minute in longitude for Mercury, then the series to the 5th power of the eccentricity will be useable for all the major planets except Pluto. The series to the 3rd power in the eccentricity gives an error in longitude of less than one arcsecond for the Earth. The series approximation has the advantage of direct use in a spreadsheet without any iteration.
Kepler's law of areas states that the area swept out by the radius vector of a planet in orbit around the sun is constant for equal periods of time. Given that the orbit for a single planet around a single massive Sun is an ellipse, this means that the planet speeds up near perihelion and slows down near aphelion.
If you want to find the position of a planet in the sky, then you need to find the position of the planet in its own orbit. You need a way of working out the longitude of the planet in its orbit at each instant.
In more precise terms, we want to find the true anomaly (v) in terms of the mean anomaly (M).
If the Sun is at one focus of the ellipse (f) and the planet is at a position (P), and perihelion (A), then the true anomaly is the angle AfP.
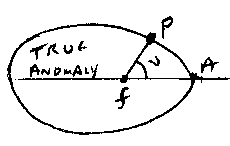
If we imagine a small circle within the orbit, and centred on the focus f, then the mean anomaly is the angle between the perihelion A, the focus f and the position the planet would occupy if it was travelling at a constant angular speed - say P1.
The mean anomaly is easily worked out from the daily motion (n) given in the orbital elements in the Astronomical Almanac.
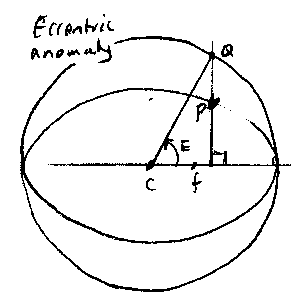
There is no obvious way to relate these two motions - but Kepler introduced a third quantity called the eccentric anomaly.
Imagine a large circle of radius equal to the semi- major axis of the orbit. Let the centre of this circle be at C. Now on the diameter of the circle which passes through the long axis of the ellipse, raise a perpendicular which meets the planet at P on the ellipse. Continue this perpendicular until it crosses the large circle. Call the point where the perpendicular crosses the large circle Q. Then the angle QCf is the eccentric anomaly E.
Kepler knew the two following relations;
E - e sin E = M (kepler's equation) tan(V/2) = sqr((1 + e)/(1 - e)) * tan(E/2)
The second formula is easy to evaluate if you know the eccentric anomaly E. The first equation is much harder to solve, as the unknown appears twice, once in a trigonometric function.
There are two main strategies - solve Kepler's equation by an iterative or trial and error method, or obtain a series for the true anomaly in terms of the mean anomaly, expanding in higher powers of the eccentricity. This latter method has become known as the 'equation of the centre'. For a full derivation of the geometry above, see Smart, Chapter 5, sections 67 -71.
We can solve Kepler's equation using an iterative procedure. In an iterative procedure, we make an initial guess, use an iteration formula to obtain an improved estimate of the eccentric anomaly, and then feed the new value into the iteration formula again to get a better guess. We stop when two successive extimates for the eccentric anomaly are equal in value to the desired accuracy. We then use the formula given above to calculate the true anomaly.
For Kepler's equation, we can use the following scheme;
E0 = M
E1 = M + ec * sin(E0)
E2 = M + ec * sin(E1)
E3 = M + ec * sin(E2)
and so on until successive estimates for E
differ by less than 0.000001 radians.
Setting up a spreadsheet to produce these successive approximations is fairly straight forward, and for Mercury (eccentricity 0.205635 from one set of osculating elements), and a mean anomaly 1.2 radians, we get the following series of approximations;
ec 0.205635
M 1.2
E1 1.391660
E2 1.402344
E3 1.402724
E4 1.402737
E5 1.402738
E6 1.402738
E7 1.402738
By the sixth iteration, the eccentric anomaly estimates coincide to within 0.0000001 radians. The formulas below should copy and paste directly into a spreadsheet in cells B1:B9;
0.205635 1.2 =$B$2+$B$1*SIN(B2) =$B$2+$B$1*SIN(B3) =$B$2+$B$1*SIN(B4) =$B$2+$B$1*SIN(B5) =$B$2+$B$1*SIN(B6) =$B$2+$B$1*SIN(B7) =$B$2+$B$1*SIN(B8)Notice the absolute referencing on eccentricity ($B$1) and mean anomaly ($B$2). In other spreadsheets, you may have to use the @ symbol or the + infront of the formulas instead of the =.
This iterative method can require a large number of iterations to converge to a good estimate for high values of the eccenricity. As an extreme example, below is some data for eccentricity = 0.999 and a mean anomaly of 150 degrees (converted to radians);
ec 0.999 M 2.617993878 E1 3.117494 E2 2.642066 E3 3.096525 E4 2.663001 E5 3.078062 E6 2.681418 E7 3.061654 E8 2.697767 E9 3.046962 E10 2.712389 E11 3.033725 E12 2.725545 E13 3.021738 E14 2.737442 E15 3.010838 E16 2.748245 E17 3.000893 E18 2.758090 E19 2.991791 E20 2.767087 E21 2.983441
As you can see, the successive estimates of eccentric anomaly are converging to two slightly different values - this is a hallmark of chaos, and indeed Kepler's equation is similar to the logistic equation. For the nine planets, these considerations don't apply, and the method will always converge to within a millionth of a radian within 8 iterations at most. See Meeus' book for more detail on the convergence of this and Newton's method.
Some spreadsheets allow 'circular references' in cell formulas. This means that you can have a formula in a cell which contains a reference to the cell which the formula is in! Microsoft Excel allows this, and gives you a section in the Tools | Options | Calculation dialog box in the iteration section (bottom right) for controlling the maximum number of iterations, and maximum change of two successive estimates. The default settings appear to be 100 iterations and 0.000001 change between estimates. This allows us to use a very simple formula to solve Kepler's equation - copy the following three lines to cells A1 to A3 of MS Excel;
0.205635 1.2 =A2+A1*SIN(A3)
The value in cell A3 should converge to 1.402737872 radians for the eccentric anomaly. This lends itself to producing an ephemeris for a planet for successive weeks or days. Be warned that a spreadsheet with a large number of these self referencing formulas can take a significant time to recalculate when changed. You may find the 'equation of centre' preferable.
In these days of cheap programmable calculators, you can find the true anomaly from the mean anomaly and the eccentricity by solving Kepler's equation by iteration.
A solution to Kepler's equation gives you the 'eccentric anomaly' (E) for the planet in an orbit of given eccentricity (ecc). You can then find the true anomaly (v) from the formula;
tan(V/2) = sqr((1 + ecc)/(1 - ecc)) * tan(E/2)
An efficient iteration scheme for solving Kepler's equation for the eccentric anomaly uses Newton's Method - and a 'manual' calculation scheme is detailed below (after Duffett- Smith, section 47).
All angles assumed in radians
To solve E - ec*sin(E) = M
eps = precision parameter, 10E-7 usually OK for
ten digit calculators, use 10E-5 if working by hand!
1) Put E = E0 = M (1st guess)
2) Find the value of d = E - ec * sin(E) - M
3) If abs(d) < eps go to step 6
else
carry on to step 4
4) find deltaE = d/(1 - ec * cos(E))
5) take new guess for E as E1 = E - deltaE
go to step 2
6) present value of E is correct within eps.
7) find tan(V/2) = sqr((1 + ec)/(1 - ec)) * tan(E/2)
8) find inverse tan, multiply by 2, and convert to degrees
for true anomaly v
The procedure above provides correct values of the true anomaly,
but can take a large number of iterations, especially for large
values of eccentricity. The method becomes unstable for certain
values of mean anomaly and eccentricity above 0.99 - chaos looms!
If you are interested in comets, then a bisection search solution
method might be more stable.
Below is a Visual Basic for Applications routine for returning
the eccentric anomaly (e) given the mean anomaly (m), the eccentricity
(ecc) and the precision parameter (eps). Note that eps is
supplied as a positive integer, and that the answer for eccentric
anomaly will be within 10^-eps of the true value.
Function kepler(m, ecc, eps)
' solves the equation e - ecc*sin(e) = m for e given an m
' returns a value of e given
' m - the 'mean anomaly' in orbit theory
' ecc - the eccentricity of the orbit
' eps - the precision parameter - solution will be
' within 10^-eps of the true value.
' don't set eps above 14, as convergence can't be guaranteed
e = m 'first guess
delta = 0.05 'set delta equal to a dummy value
Do While Abs(delta) >= 10 ^ -eps 'converged?
delta = e - ecc * Sin(e) - m 'new error
e = e - delta / (1 - ecc * Cos(e)) 'corrected guess
Loop
kepler = e 'return estimate
End Function
To use the function above in Excel, you need to insert a new
module into your Excel workbook, and then copy the text into the
blank module window. Within that workbook, you can then use
kepler() just like any other function.
The QBASIC function below returns the true
anomaly (v) when given the mean anomaly (m), the eccentricity of
the orbit (ecc) and a precision parameter (eps). The similarity
in syntax between this QBASIC function and the
Visual Basic for Applications function above is obvious - you can
'testbed' ideas in QBASIC and transfer them to Excel
later.
FUNCTION kepler (m, ecc, eps)
' returns the true anomaly given
' m - the mean anomaly in radians
' ecc - the eccentricity of the orbit
' eps - the convergence paramter (8 or 9 is usually fine
' 12 or 14 for very accurate work)
e = m
delta = .05#
twopi = 8 * ATN(1)
DO WHILE ABS(delta) >= 10 ^ -eps
delta = e - ecc * SIN(e) - m
e = e - delta / (1 - ecc * COS(e))
LOOP
v = 2 * ATN(((1 + ecc) / (1 - ecc)) ^ .5 * TAN(.5 * e))
IF v < 0 THEN v = v + twopi
kepler = v
END FUNCTION
The TI-80 programmable calculator is a cheap basic machine with about 6K of memory. That does not sound much (about one Windows icon!) but it is enough to program a whole series of astronomical routines. Similar machines are available in the Cassio and Sharp range, and most cost less than 30 Pounds Sterling.
The TI-80 programming language has a very simple syntax, and
loops are constructed using the goto label method.
However, it is possible to call programs from within other
programs, so some kind of structured approach is possible. All
variables are global - and you only have 26 memories
(A to Z) and six 'lists' each of which
can hold 100 numbers.
The sub-program below will return a value for the true anomaly
in memory V, given the eccentricity of the orbit in
memory A, and the mean anomaly in memory
M.
Conventions used in listing
The TI-80 screen has a 'proper' pi symbol - I use 'pi'
to represent the circle constant here.
I use 'TAN-1' here to mean 'inverse tan' function, again
the TI-80 has a better screen representation of this.
I have added comments on most lines - of course there
is NO comment function on the TI-80!
I use the symbol --> to stand for the assignment
arrow. In TI-80 language, assignment is done 'right to left'
so that 'A --> B' assigns the value of memory A to
memory B.
PROGRAM:ZKEPLER
:pi * M/180 -->B 'first guess set to eccentric anomaly
'store mean anom in B as rads for later
:RADIAN 'runs rest of routine in radians
:LBL 1 'label 1 - target for a later goto 8-{
:E - A * SIN(E) - B --> X 'find difference
:IF ABS(X) <= 0.0000001 goto 2 'quit loop if converged
:E - x/(1 - A * COS(E)) --> E 'new value of E
:GOTO 1 'loop for next iteration
:LBL 2 'target for goto in loop
:2 * TAN-1(((1+A)/(1-A))^0.5 * TAN(E/2)) --> V
:V * 180/pi --> V 'convert V back to degrees
:DEGREE 'switch back to degree mode
:RETURN 'back to calling program
Newton's method for iterative solution of equations is a standard technique and you will find accounts of the method in most books on numerical analysis see Numerical Recipes in C, section 9.4 for example.
For certain kinds of function, the method either does not converge, or generates very large values before converging. Large values can 'overflow' calculators and computers.
In the case of Kepler's equation, the iterative routines
shown here converge very rapidly - within a maximum of 8 loops -
for all values of eccentricity less than about 0.99. Above this
value of eccentricity, and for certain values of mean anomaly,
there will be problems with convergence, especially with the 10
decimal digit accuracy on the TI-80. The VBA and
QBASIC routines work in 'double precision' and will
normally converge over a large range of eccentricity.
Meeus (page 189, table 29.B) gives a set of test
data for his HP-85 computer (nostalgia!) and finds that he needs
47 steps to obtain convergence in an orbit with eccentricity of
0.999, and a mean anomaly of 7 degrees. Both the VBA and the
QBASIC routines handled this case, but the TI-80
gave an overflow error on iteration 53 with E = 2 *
10^9. Your mileage may vary.
To repeat my earlier comment, if you are working with orbits of eccentricity above 0.9, it would be best to use a bisection search method, or even use a parabolic orbit approximation.
The equation of centre seems to be the name given to series which give an approximation to the true anomaly directly in terms of the mean anomaly. These series are power series in the eccentricity, and trigonometric series in multiples of the mean anomaly. Smart Chapter V, sections 72, 73 gives a derivation for the series form of the equation of centre. This derivation seems quite complex, and I shall try to find a simpler one when I have time for some real maths!
The Astronomical Almanac gives the following version of the equation of centre to the third power in eccentricity - see page E4 in the 1997 issue.
v = M + (2e - 0.25*e^3)*sin(M) + 1.25*e^2*sin(2*m) + 13/12* e^3* sin(3*M) where all angles are in radians
I rearranged the series as a polynomial in the eccentricity
(for any given calculation, the sin terms are
constants) and used an old trick for evaluating polynomials
without finding powers directly - (see Meeus, Chapter 1,
page 11 or Numerical Recipes in C, 5.3). The
resulting QBASIC is shown below;
FUNCTION kep3a (m, e, eps) 'uses the equation of centre in the Astronomical Almanac 1997 'page E4 as modified to make it more efficient m1 = SIN(m) m2 = SIN(2 * m) m3 = SIN(3 * m) a1 = 2 * m1 a2 = 1.25 * m2 a3 = -.25 * m1 + 1.083333333# * m3 kep3a = m + e * (a1 + e * (a2 + e * a3)) END FUNCTIONYou could probably save the
m2 variable, but keeping it
makes the listing a bit clearer.
A series expansion up to the 5th power in eccentricity gives an approximation to the true anomaly in terms of the mean anomaly. Meeus (Chapter 32, page 222) gives the series for the difference between the mean anomaly M and the true anomaly v. I state the series for the true anomaly in radians;
v = M + (2 * e - 0.25 * e^3 + 5/96 * e^5) * sin(M)
+ (1.25 * e^2 - 11/24 * e^4) * sin(2*M)
+ (13/12 * e^3 - 43/64 * e^5) * sin(3*M)
+ 103/96 * e^4 * sin(4*M)
+ 1097/960 * e^5 * sin(5*M)
And below is a QBASIC function - I have re-arranged
the formula to make the computation more efficient. I have also
used decimal approximations to the coefficients. I have found no
problems doing this, and the procedure saves a number of divide
operations.
FUNCTION kep5a (m, e, ep) ' equation of centre with terms up to fifth power of ' the eccentricity. Meeus p222. ' needs 5 sin calls, 19 add/subtracts, 14 mults ' per call. s1 = SIN(m) s2 = SIN(m + m) s3 = SIN(m + m + m) s4 = SIN(m + m + m + m) s5 = SIN(m + m + m + m + m) 'probably going over the top here! a1 = 2 * s1 a2 = 1.25 * s2 a3 = 1.083333333# * s3 - .25 * s1 a4 = 1.072916667# * s4 - .4583333333# * s2 a5 = .0520833333# * s1 - .671875# * s3 + 1.142708333# * s5 kep5a = m + e * (a1 + e * (a2 + e * (a3 + e * (a4 + e * a5)))) END FUNCTION
Using the QBASIC interpreter, double precision
additions are marginally faster than multiplies, so I used
repeated addition in the calls to the SIN function.
This is probably pointless!
I wrote a simple QBASIC program to compare the
values of true anomaly produced using the two versions of the
Equation of Centre with the values obtained from the iterative
solution to Kepler's equation. I found the value of the true
anomaly produced by each method for each degree of mean anomaly
for values of mean anomaly from 0 degrees up to 180 degrees.
The 'error' for each version of the Equation of Centre is defined as 'kepler - Eq Centre' and is expressed in arcseconds. The program kept the largest value of error seen for each of the two series. In the table below, c3 represents the error from using the 3rd power of eccentricity, and c5 is the error for the 5th power of eccentricity.
Maximum errors in true anomaly arcseconds
Eccen c3 c5
Venus 0.006773 0 0
Uranus 0.008606 0 0
Sun 0.016709 0 0
Neptune 0.047318 1 0
Jupiter 0.048489 2 0
Moon 0.054900 3 0
Saturn 0.055546 3 0
Mars 0.093405 23 0
Mercury 0.205635 540 35
As you can see from the table, Mars and Mercury are the two planets most liable to errors in true anomaly by the use of the Equation of centre. If you want to produce a simple program to find the positions of the planets in the sky, then the c3 series will probably be useable, but positions for Mercury may be in error by 9 minutes of arc.
Newton's method may be expected to take longer to calculate.
The time taken for each function call will also depend on the
number of iterations which are needed to converge to the
precision value needed. I produced the following comparative
timings using a Pentium 75 MHz computer with interpreted
QBASIC running in a DOS session window under Windows
95. The program evaluated the true anomaly for each degree of
mean anomaly between 0 degrees and 360 degrees, repeating
the loop 10 times. Each function is called 3600 times, with a
variety of input values. The Newton's method was set to a
precision of 10^-12 in all the runs below;
Time in seconds for 3600 function calls
eccentricity values
0.25 0.1 0.05 0.9
Newton's method 26.9 24.9 23.9 33.8
c5 series 8.3 8.3 8.4 8.5
c3 series 4.8 5.0 4.9 4.9
QBASIC - relative times may change on other interpreters
and systems.
As might be expected each equation of centre series function took more or less the same time to return a value irrespective of the value of the eccentricity. The values for true anomaly returned by these functions for eccentricities much over 0.25 will be very inaccurate.
The Newton's method function takes about six times longer than
the c3 power series, and the time does depend on the value of
eccentricity to some extent, but less than might be expected. The
true anomaly values generated by this function will be accurate
to 10^-12 of a radian.
I have chosen to use the Newton's Method function on my TI-80, but may use the c5 series on a spreadsheet, as the series dispenses with the need to use a 'macro' function.
If you need to squeeze the most speed from your programs, then using the c3 series for the Sun/Earth orbit (which is needed to find geocentric positions of any other body) may eliminate a call to the Kepler routine.
Below is a list of the books which I have used in compiling this page. These books should be found in most University libraries in English speaking countries.
Duffett-Smith, Peter
Practical Astronomy with your calculator
Cambridge University Press
3rd edition 1988
ISBN 0-521-35699-7
Meeus, Jean
Astronomical Algorithms
Willmann-Bell
1st English edition, 1991
ISBN 0-943396-35-2
Press, Flannery, Teukolsky, Vetterling
Numerical recipes in C
Cambridge University Press
1st ed 1988
ISBN 0-521-35465-X
Smart, W,M,
Text Book of Spherical Astronomy
Cambridge University Press
6th ed
[Root]
Last Modified 1st November 1998
Keith Burnett