Converting from polar to rectangular coordinates

This page contains a detailed description of the derivation of the formulas for the equatorial rectangular coordinates of a star from the RA and the DEC. If you know the basic trigonometry of a right angled triangle, you should have no special problems with this section.

The system of rectangular coordinates used has;

• the Z axis pointing towards the North Celestial Pole, so the XY plane is the plane of the equator
• the X axis points towards the zero for RA (the so-called 'first point of Aries').
• the Y axis direction is now fixed, as it must be in the plane of the equator, at right angles to the X axis, and in the direction consistent with a right handed set of axes.

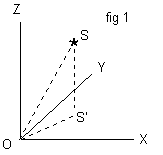
We assume that the stars are all at the same distance from the centre of the celestial sphere, and we may as well call that distance 1 unit. Suppose we call the origin of our set O, and suppose a star is at S, so the line OS has length 1 unit. You can work out the x, y, and z coordinates of the star using nothing more than the trigonometry of two right angled triangles. The situation is shown in fig 1 if you are using a graphical browser to view these pages;

The Z coordinate of the star's position is equal to the length of a line dropped down from the star to the XY plane. Call the point in the XY plane directly underneath the star S'. The Z coordinate of the star is now the length SS' (see fig 1).

We now have a right angled triangle with hypotenuse OS (see fig 2 below for a clearer view of the triangle).

• The angle between the line OS' and OS is just the declination of the star.
• So the length of OS' must be cos(dec)
• The length SS', which is the z coordinate of the star's position, is sin(dec).

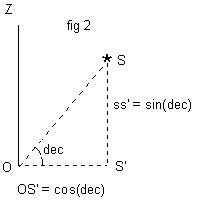
To get the values of the Y and X coordinates, we need to look at another triangle, in the XY plane (see fig 3). You need to imagine that the Z axis is pointing out of the screen.

• The triangle formed by the lines OS', S'x and xO make a right angled triangle, and the angle at O is just the right ascension - RA measures 'how far round' the star is from the Y axis.
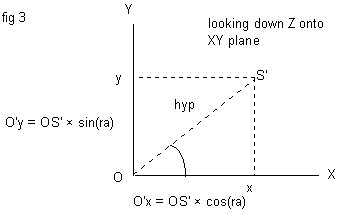
• The hypotenuse of this triangle is the line OS', which has length cos(dec). Applying trigonometry to the situation gives us;
• Ox = OS' * cos(ra) = cos(ra)*cos(dec), and this is the X coordinate of the star
• Oy = OS' * sin(ra) = sin(ra)*cos(dec), and this is the Y coordinate of the star

Summarising these results we get;

    X = cos(ra) * cos(dec)
    Y = sin(ra) * cos(dec)
    Z = sin(dec)

You may not be at all surprised to learn that the same reasoning applies to geocentric ecliptic coordinates. This time the axes are;

• the Z axis pointing towards the North ecliptic pole, so the XY plane is the plane of the ecliptic
• the X axis points towards the zero for ecliptic longitude. No change here, the 'first point of Aries' is one of the two points on the celestial sphere where the Ecliptic and Equator cross, so these two systems share a common axis.
• the Y axis direction is now fixed, as it must be in the plane of the ecliptic, at right angles to the X axis, and in the direction consistent with a right handed set of axes.

We get the following formulas (where L is ecliptic longitude and B is ecliptic latitude)

    X = cos(L) * cos(B)
    Y = sin(L) * cos(B)
    Z = sin(B)

[Root] [Branch]

Last Modified 6th September 1998
Keith Burnett